Derivatives for logistic regression - step by step
Motivation
The training step in logistic regression involves updating the weights and the bias by a small amount. The amount that each weight and bias is updated by is proportional to the gradients, which are calculated as the partial derivative of the loss function, with respect to the weight (or bias) we are updating.
This blog post will cover how to calculate the partial derivatives of the weights and the bias, step by step. I would recommend reading my previous two blog posts which cover how to perform derivatives along a computational graph and the derivative of the sigmoid function.
Logistic Regression computational graph
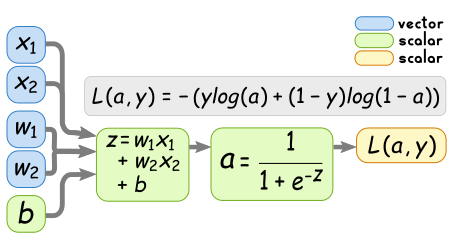
The computational graph of logistic regression can be visualised as follows:

w and x are vectors, whose size depend on the number of input
features. In order to keep things simple, we will consider the case
where we only have two input features. We can therefore represent the
computational graph more clearly as follows:
Desired partial derivatives
The partial derivatives we are particularly interested are the following two:

Strategy for solving partial derivatives
In order to solve the partial derivatives, we can make use of the chain rule, which allows us to simplify the process by considering small components at a time.
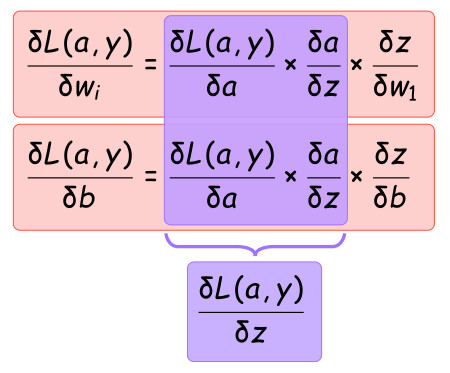
Which can be visualised on the computational graph as follows:
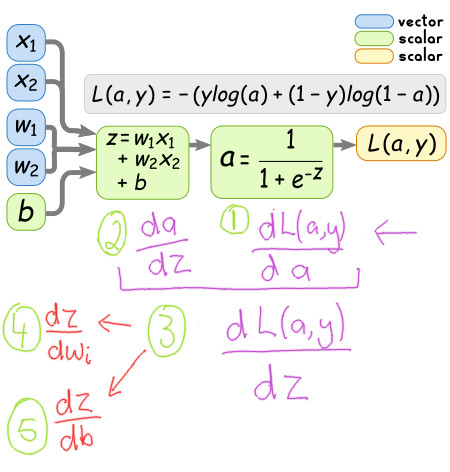
Once we calculate those five smaller components, we can solve the partial derivatives we want more easily. So lets start solving each compoment.
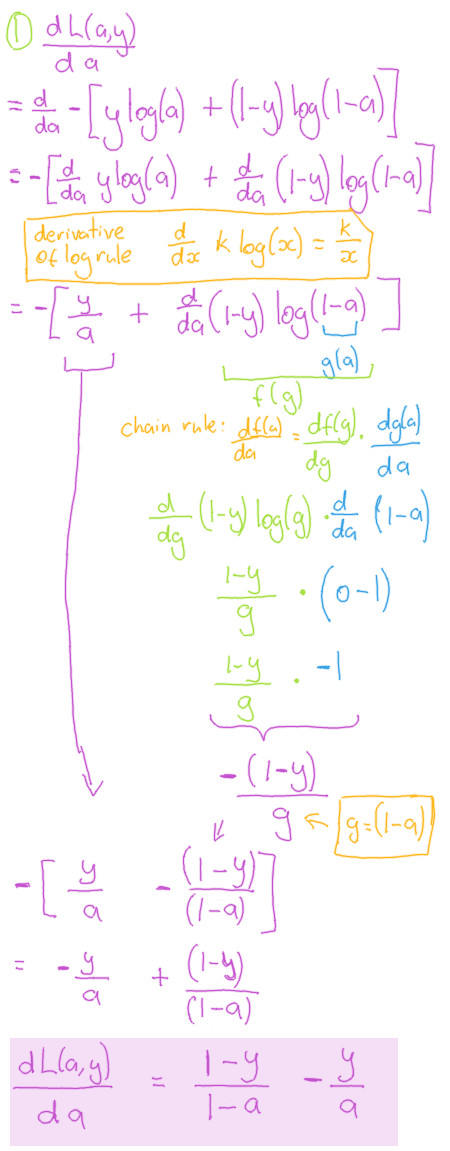
Compoment 1
Be aware that the logs used in the loss function are natural logs, and not base 10 logs.
Compoment 2
The full calculation of this component was explained in my previous blog post for calculating the derivative of the sigmoid function. Be sure to check out that post if you want to know how it was calculated.
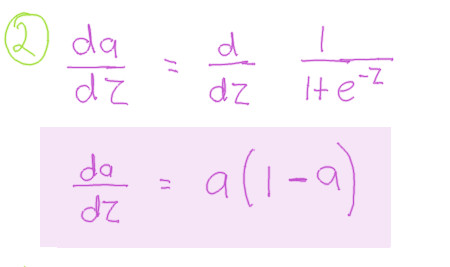
Compoment 3
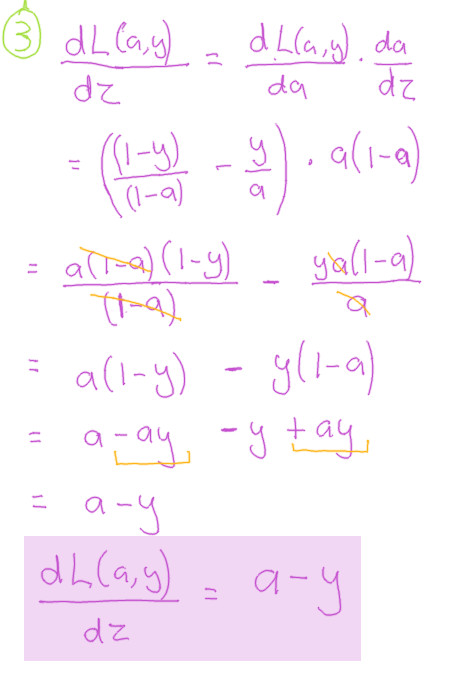
Compoment 4
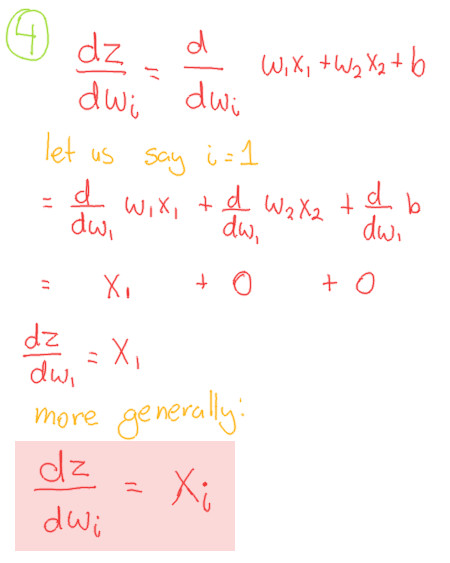
Compoment 5
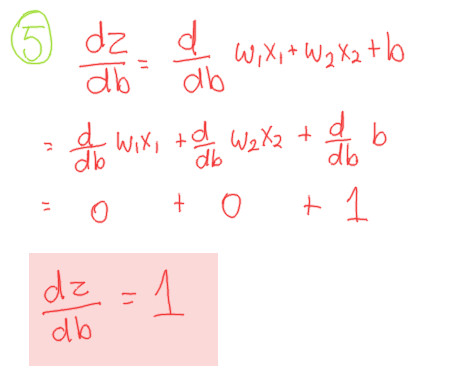
Putting the components together
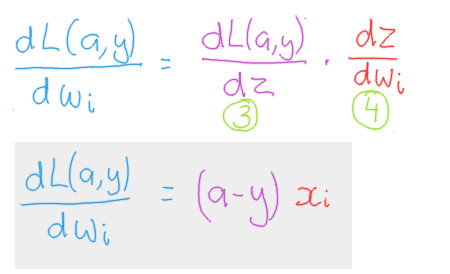
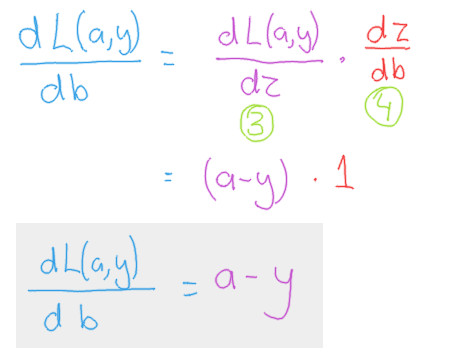
The final product
To summarize, the derivatives we are interested have been summarized in the following two formulas.
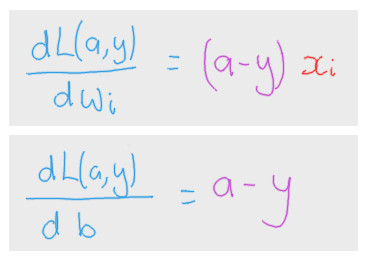
Comments
Note you can comment without any login by:
- Typing your comment
- Selecting "sign up with Disqus"
- Then checking "I'd rather post as a guest"