1. Summary

This post will cover how to avoid headaches with Tensorflow's built in evaluation metrics operations such as

• tf.metrics.accuracy()
• tf.metrics.precision()
• tf.metrics.recall()
• tf.metrics.mean_iou()
• and others

Even though I will use tf.metrics.accuracy() in the examples to keep things simple, the pattern for using it, and the intuitions for what it does behind the scenes will apply to all the evaluation metrics.

If you just want to skip to the example code on how to use the metrics, then jump to section 5.1 and 5.2, otherwise, if you want to get a good intuition for why it is used this way, please read on.

This post will go through a very simple coding example in which we create our own evaluation metric using Numpy. This will give you a good intuition for how the evaluation metrics in Tensorflow work. Once this intuition has been built, we look at what the equivalent compo

But first, let me provide the rationale for why I created this post in the first place.

2. Background

The rationale for this post comes from attempting to use the tf.metrics.mean_iou() evaluation metric for image segmentation, and getting completely strange and incorrect results. I spent a day and a half banging my head up against the wall in frustration figuring out what I did wrong.

It is quite easy to use the evaluation metrics incorrectly, and the difference between doing it correctly and incorrectly is quite subtle. As of the 11th of September 2017, the tensorflow documentation does not make it very clear how to use Tensorflow's evaluation metrics correctly.

This post, therefore, is intended to help other people avoid the same headache I had, and also give a good intuition for what is going on behind the scenes to get an understanding of why it is used the way it is used.

3. The data to be used

Before we start with any evaluation metrics, let us start with the simple data we will use. We will use the following Numpy arrays as our predicted labels, and our ground truth labels.

Let's treat each row as being a batch of labels/predictions, so we have four such batches.

import numpy as np
labels = np.array([[1,1,1,0],
                   [1,1,1,0],
                   [1,1,1,0],
                   [1,1,1,0]], dtype=np.uint8)

predictions = np.array([[1,0,0,0],
                        [1,1,0,0],
                        [1,1,1,0],
                        [0,1,1,1]], dtype=np.uint8)

n_batches = len(labels)

4. Intuition pump - building our own evaluation metric

To keep things simple, let's suppose the evaluation metric we are interested in is accuracy. Accuracy is just defined as:

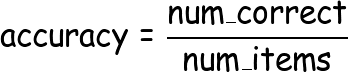
If we want to calculate the accuracy over the entire set of batches, then we might try something like this:

n_items = labels.size
accuracy = (labels ==  predictions).sum() / n_items
print("Accuracy :", accuracy)

[OUTPUT]
Accuracy : 0.6875

The problem with this approach is that it is not not scalable to large datasets that are too big to fit into memory in one go. In order to make it scalable, we would like to make the evaluation metric capable of updating itself incrementally, with each new batch of predictions and labels. To do this, we will need to keep track of two values.

• The sum of correctly predicted items
• The total number of items we have seen

In Python, we could store these like follows:

# Initialize running variables
N_CORRECT = 0
N_ITEMS_SEEN = 0

Every time we come accross a new batch of items, we would need to perform an update operation on these variables. This would look like:

# Update running variables
N_CORRECT += (batch_labels == batch_predictions).sum()
N_ITEMS_SEEN += batch_labels.size

Now, in order to calculate the accuracy at any point in time, we would simply do:

# Calculate accuracy on updated values
acc = float(N_CORRECT) / N_ITEMS_SEEN

If we were to put these components into their own separate functions and put it all together, we would get something like this:

# Create running variables
N_CORRECT = 0
N_ITEMS_SEEN = 0

def reset_running_variables():
    """ Resets the previous values of running variables to zero """
    global N_CORRECT, N_ITEMS_SEEN
    N_CORRECT = 0
    N_ITEMS_SEEN = 0

def update_running_variables(labs, preds):
    global N_CORRECT, N_ITEMS_SEEN
    N_CORRECT += (labs == preds).sum()
    N_ITEMS_SEEN += labs.size

def calculate_accuracy():
    global N_CORRECT, N_ITEMS_SEEN
    return float(N_CORRECT) / N_ITEMS_SEEN

4.1 Overall accuracy, one batch at a time

Actually making use of the functions defined in section 4 to calculate the overall accuracy of the entire dataset would look something like:

reset_running_variables()

for i in range(n_batches):
    update_running_variables(labs=labels[i], preds=predictions[i])

accuracy = calculate_accuracy()
print("[NP] SCORE: ", accuracy)

[OUTPUT]
[NP] SCORE:  0.6875

4.2 Batch accuracy

If on the other hand, we wanted to calculate the accuracy of each batch separately, then we would arrange the functions differently. We would reset the running variables to zero before each new batch of data.

for i in range(n_batches):
    reset_running_variables()
    update_running_variables(labs=labels[i], preds=predictions[i])
    acc = calculate_accuracy()
    print("- [NP] batch {} score: {}".format(i, acc))

[OUTPUT]
- [NP] batch 0 score: 0.5
- [NP] batch 1 score: 0.75
- [NP] batch 2 score: 1.0
- [NP] batch 3 score: 0.5

5. In Tensorflow

The way the operations were been split up into different functions in section 4, is very similar to the way the Tensorflow metrics operations have been split up.

When we call the tf.metrics.accuracy() function, several things are happening. (The equivalent variable or function from the simple example of section 4 is put in brackets).

1. Two running variables are created and placed into the computational graph behind the scenes.
   • total (equivalent to N_CORRECT)
   • count (equivalent to N_ITEMS_SEEN)
2. Two tensorflow operations are returned.
   • accuracy (equivalent to calculate_accuracy() )
   • update_op (equivalent to update_running_variables())

In order to initialize and reset the running variables, like the reset_running_variables() function from section 4, we first need to isolate the running variables (total and count). A good way of doing this is to explicitly assign a name to the tf.metrics.accuracy() function when calling it in the first place, eg:

tf.metrics.accuracy(label, prediction, name="my_metric")

And then isolating the running variables by searching for variables whose names contain our evaluation metric as part of its scope.

# Isolate the variables stored behind the scenes by the metric operation
running_vars = tf.get_collection(tf.GraphKeys.LOCAL_VARIABLES, scope="my_metric")

running_vars will store the following two tensorflow variables:

<tf.Variable 'my_metric/total:0' shape=() dtype=float32_ref>,
<tf.Variable 'my_metric/count:0' shape=() dtype=float32_ref>

Now, we need to specify an operation that will perform the initialization/resetting of those running variables.

running_vars_initializer = tf.variables_initializer(var_list=running_vars)

To actually initialize/reset the values, we need to call this initializer operation within a Tensorflow session, using:

session.run(running_vars_initializer)

SIDE NOTE: Instead of isolating the running variables manually and initializing them directly, some people reset the variables by running.

session.run(tf.local_variables_initializer())

The problem with doing it this way is that depending on your graph, there might be other variables that you might accidentally reset unintentionally. By being explicit about which variables we want to reset, we avoid other potential bugs in the system.

The next two subsections will make all this clearer, as we apply it to the sample data.

5.1 Tensorflow - overall accuracy, one batch at a time

In order to calculate the overall accuracy of the entire dataset (but processing the data in batches) it would look something like this:

import tensorflow as tf

graph = tf.Graph()
with graph.as_default():
    # Placeholders to take in batches onf data
    tf_label = tf.placeholder(dtype=tf.int32, shape=[None])
    tf_prediction = tf.placeholder(dtype=tf.int32, shape=[None])

    # Define the metric and update operations
    tf_metric, tf_metric_update = tf.metrics.accuracy(tf_label,
                                                      tf_prediction,
                                                      name="my_metric")

    # Isolate the variables stored behind the scenes by the metric operation
    running_vars = tf.get_collection(tf.GraphKeys.LOCAL_VARIABLES, scope="my_metric")

    # Define initializer to initialize/reset running variables
    running_vars_initializer = tf.variables_initializer(var_list=running_vars)


with tf.Session(graph=graph) as session:
    session.run(tf.global_variables_initializer())

    # initialize/reset the running variables
    session.run(running_vars_initializer)

    for i in range(n_batches):
        # Update the running variables on new batch of samples
        feed_dict={tf_label: labels[i], tf_prediction: predictions[i]}
        session.run(tf_metric_update, feed_dict=feed_dict)

    # Calculate the score
    score = session.run(tf_metric)
    print("[TF] SCORE: ", score)

[OUTPUT]
[TF] SCORE:  0.6875

5.2 Tensorflow - Batch accuracy

In order to calculate the accuracy of each batch separately, we would arrange the operations differently. We would reset the running variables to zero before each new batch of data.

The graph specification will be the same as for section 5.1, so I have only included the session code.

with tf.Session(graph=graph) as session:
    session.run(tf.global_variables_initializer())

    for i in range(n_batches):
        # Reset the running variables
        session.run(running_vars_initializer)

        # Update the running variables on new batch of samples
        feed_dict={tf_label: labels[i], tf_prediction: predictions[i]}
        session.run(tf_metric_update, feed_dict=feed_dict)

        # Calculate the score on this batch
        score = session.run(tf_metric)
        print("[TF] batch {} score: {}".format(i, score))

[OUTPUT]
[TF] batch 0 score: 0.5
[TF] batch 1 score: 0.75
[TF] batch 2 score: 1.0
[TF] batch 3 score: 0.5

5.3 Avoiding headaches

Do not call the tf_metric and tf_metric_update in the same session.run() function call, as in either of the following two lines:

_ , score = session.run([tf_metric_update, tf_metric], feed_dict=feed_dict)

score, _ = session.run([tf_metric, tf_metric_update], feed_dict=feed_dict)

In Tensorflow version 1.3 (and potentially other versions), this will give you very inconsistent and mostly incorrect results. Most of the time it will return zeros, occasionally the correct answer, and sometimes some seemingly random value.

6. Other metrics

The other evaluation metrics in tf.metrics will work in the same sort of way. The only difference between them might be extra arguments needed when calling the tf.metrics function. For example, tf.metrics.mean_iou() requires an additional argument num_classes for the number of possible classes.

The only other difference will be the variables that are stored in the background, but they can still be collected and initialized in the same way that I have described in section 5 of this post.